Options Valuation

Options

An option is a contract that gives a person or institution the right to buy or sell an asset at a specified price. A call option is a contract to buy an asset at a fixed price while a put option is a contract to sell an asset at a fixed price. The specified price is known as the option's strike price or exercise price. Options come with an expiration date where it can no longer be exercised. This date is also known as the maturity date. There are two important types of options, the American type and the European type. The American type option can be exercised any time up to the expiration date whereas the European type of option can only be exercised on the expiration date. One important usage of option is to adjust the risk exposure an investor has to the underlying assets.

Options Valuation spreadsheet

This spreadsheet uses the Put Call Parity relation, Binomial Option Pricing and Black Scholes model to value options.

Put Call Parity

 The Put Call Parity assumes that options are not exercised before expiration day which is a necessity in European options. It defines a relationship between the price of a call option and a put option with the same strike price and expiry date, the stock price and the risk free rate.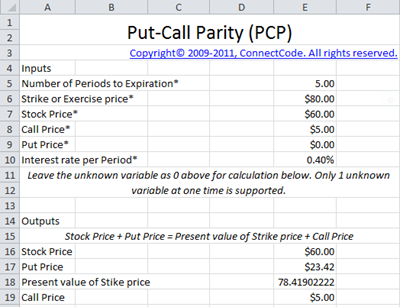


The spreadsheet supports the calculation of the Stock Price, Put Price, Present value of Strike Price or Call Price depending on the input values provided. Simply leave the unknown variable as 0 and it will automatically be calculated by the program. Do note that only one unknown variable is supported at one time.



Binomial Option Pricing

 For many years, financial analysts have difficulty in developing a rigorous method for valuing options. This is until Fisher Black and Myron Scholes published the article "The Pricing of Options and Corporate Liabilities" in 1973 to describe a model for valuing options. This model is famously known as the Black Scholes model. The Black Scholes model can be easily understood through a Binomial Option Pricing model. The model has a name "Binomial" because of its assumptions of having two possible states. Basically, the Binomial Option Pricing and Black Scholes models use the simple idea of setting up a replicating portfolio which replicates the payoff of the call or put option. The value of the portfolio is then observed to be the value or cost of the options.

Binomial Option Pricing - Call Option

This worksheet sets up a replicating portfolio by borrowing money at the risk free rate and purchasing an amount of the actual stock to replicate the payoff of the Call Option. It then calculates the value (price) of the Call Option through observing the value of the portfolio.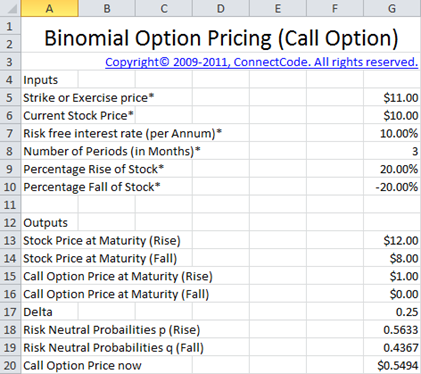


Binomial Option Pricing - Put Option

This worksheet sets up a replicating portfolio by lending money at the risk free rate and selling an amount of the actual stock to replicate the payoff of the Put Option. It then calculates the value (price) of the Put Option through observing the value of the portfolio.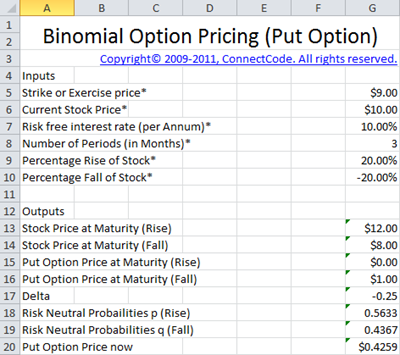


Black Scholes Model

 The Black Scholes Model is similar to that of the Binomial Option Pricing. The Binomial Option Pricing assumes two possible values of the stock price at the end of the period (maturity). If we initially used 1 year as the end of period and subsequently shorten the period to half a year, the number of possible values at the end of year increases. By further shortening the period, we get an increasing number of possible values at the end of the year. We will reach a stage where we have a continuous range of possible prices at the end of the year. The Black Scholes Model provides a formula for calculating the value of the option (or portofolio) in the situation above and thus allows us to easily value options.





Download Free Options Valuation spreadsheet - v1.0

 System Requirements

Microsoft® Windows 7, Windows 8 or Windows 10
Windows Server 2003, 2008, 2012 or 2016
512 MB RAM
5 MB of Hard Disk space
Excel 2007, 2010, 2013 or 2016

License

By downloading this software from our web site, you agree to the terms of our license agreement.

Download

FreeOptionsValuation.zip (Zip Format - 98 KB)

Get the Professional version

 Benefits Details PDF Specifications Commercial license

Price - Limited Time Only!

USD30.00 - Purchase

Note - If you are the user of a previous version (of the Professional Options Valuation package), please contact us for your free upgrade.